Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 8 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 8 Maths Book syllabus.

1. Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14 pq, 28p2 q2
(iv) 2x, 3x2 , 4
(v) 6 abc, 24ab2 , 12a2 b
(vi) 16 x3 , – 4x2 , 32 x
(vii) 10 pq, 20qr, 30 rp
(viii) 3x2 y3 , 10x3 y2 , 6x2 y2 z
Solution:
(i) Factors of 12x and 36
12x = 2×2×3×x
36 = 2×2×3×3
Common factors of 12x and 36 are 2, 2, 3
and , 2×2×3 = 12
(ii) Factors of 2y and 22xy
2y = 2×y
22xy = 2×11×x×y
Common factors of 2y and 22xy are 2, y
and ,2×y = 2y
(iii) Factors of 14pq and 28p2 q2
14pq = 2x7xpxq
28p2 q2 = 2x2x7xpxpxqxq
Common factors of 14 pq and 28 p2 q2 are 2, 7 , p , q
and, 2x7xpxq = 14pq
(iv) Factors of 2x, 3x2 and 4
2x = 2×x
3x2 = 3×x×x
4 = 2×2
Common factors of 2x, 3x2 and 4 is 1.
(v) Factors of 6abc, 24ab2 and 12a2 b
6abc = 2×3×a×b×c
24ab2 = 2×2×2×3×a×b×b
12 a2 b = 2×2×3×a×a×b
Common factors of 6 abc, 24ab2 and 12a2 b are 2, 3, a, b
and, 2×3×a×b = 6ab
(vi) Factors of 16x3 , -4x2 and 32x
16 x3 = 2×2×2×2×x×x×x
– 4x2 = -1×2×2×x×x
32x = 2×2×2×2×2×x
Common factors of 16 x3 , – 4x2 and 32x are 2,2, x
and, 2×2×x = 4x
(vii) Factors of 10 pq, 20qr and 30rp
10 pq = 2×5×p×q
20qr = 2×2×5×q×r
30rp= 2×3×5×r×p
Common factors of 10 pq, 20qr and 30rp are 2, 5
and, 2×5 = 10
(viii) Factors of 3x2 y3 , 10x3 y2 and 6x2 y2 z
3x2 y3 = 3×x×x×y×y×y
10x3 y2 = 2×5×x×x×x×y×y
6x2 y2 z = 3×2×x×x×y×y×z
Common factors of 3x2 y3 , 10x3 y2 and 6x2 y2 z are x2 , y2
and, x2 ×y2 = x2 y2
2.Factorise the following expressions.
(i) 7x–42
(ii) 6p–12q
(iii) 7a2 + 14a
(iv) -16z+20 z3
(v) 20l2 m+30alm
(vi) 5x2 y-15xy2
(vii) 10a2 -15b2 +20c2
(viii) -4a2 +4ab–4 ca
(ix) x2 yz+xy2 z +xyz2
(x) ax2 y+bxy2 +cxyz
Solution:


(vii) 10a2 -15b2 +20c2
10a2 = 2×5×a×a
– 15b2 = -1×3×5×b×b
20c2 = 2×2×5×c×c
Common factor of 10 a2 , 15b2 and 20c2 is 5
10a2 -15b2 +20c2 = 5(2a2 -3b2 +4c2 )
(viii) – 4a2 +4ab-4ca
– 4a2 = -1×2×2×a×a
4ab = 2×2×a×b
– 4ca = -1×2×2×c×a
Common factor of – 4a2 , 4ab , – 4ca are 2, 2, a i.e. 4a
So,
– 4a2 +4 ab-4 ca = 4a(-a+b-c)
(ix) x2 yz+xy2 z+xyz2
x2 yz = x×x×y×z
xy2 z = x×y×y×z
xyz2 = x×y×z×z
Common factor of x2 yz , xy2 z and xyz2 are x, y, z i.e. xyz
Now, x2 yz+xy2 z+xyz2 = xyz(x+y+z)
(x) ax2 y+bxy2 +cxyz
ax2 y = a×x×x×y
bxy2 = b×x×y×y
cxyz = c×x×y×z
Common factors of a x2 y ,bxy2 and cxyz are xy
Now, ax2 y+bxy2 +cxyz = xy(ax+by+cz)
3. Factorise.
(i) x2 +xy+8x+8y
(ii) 15xy–6x+5y–2
(iii) ax+bx–ay–by
(iv) 15pq+15+9q+25p
(v) z–7+7xy–xyz
Solution :

1. Factorise the following expressions.
(i) a2 +8a+16
(ii) p2 –10p+25
(iii) 25m2 +30m+9
(iv) 49y2 +84yz+36z2
(v) 4x2 –8x+4
(vi) 121b2 –88bc+16c2
(vii) (l+m)2 –4lm (Hint: Expand (l+m)2 first)
(viii) a4 +2a2 b2 +b4
Solution:
(i) a2 +8a+16
= a2 +2×4×a+42
= (a+4)2
Using the identity (x+y)2 = x2 +2xy+y2
(ii) p2 –10p+25
= p2 -2×5×p+52
= (p-5)2
Using the identity (x-y)2 = x2 -2xy+y2
(iii) 25m2 +30m+9
= (5m)2 +2×5m×3+32
= (5m+3)2
Using the identity (x+y)2 = x2 +2xy+y2
(iv) 49y2 +84yz+36z2
=(7y)2 +2×7y×6z+(6z)2
= (7y+6z)2
Using the identity (x+y)2 = x2 +2xy+y2
(v) 4x2 –8x+4
= (2x)2 -2×4x+22
= (2x-2)2
Using the identity (x-y)2 = x2 -2xy+y2
(vi) 121b2 -88bc+16c2
= (11b)2 -2×11b×4c+(4c)2
= (11b-4c)2
Using the identity (x-y)2 = x2 -2xy+y2
(vii) (l+m)2 -4lm (Hint: Expand (l+m)2 first)
Expand (l+m)2 using the identity (x+y)2 = x2 +2xy+y2
(l+m)2 -4lm = l2 +m2 +2lm-4lm
= l2 +m2 -2lm
= (l-m)2
Using the identity (x-y)2 = x2 -2xy+y2
(viii) a4 +2a2 b2 +b4
= (a2 )2 +2×a2× b2 +(b2 )2
= (a2 +b2 )2
Using the identity (x+y)2 = x2 +2xy+y2
2. Factorise.
(i) 4p2 –9q2
(ii) 63a2 –112b2
(iii) 49x2 –36
(iv) 16x5 –144x3 differ
(v) (l+m)2 -(l-m)2
(vi) 9x2 y2 –16
(vii) (x2 –2xy+y2 )–z2
(viii) 25a2 –4b2 +28bc–49c2
Solution:
(i) 4p2 –9q2
= (2p)2 -(3q)2
= (2p-3q)(2p+3q)
Using the identity x2 -y2 = (x+y)(x-y)
(ii) 63a2 –112b2
= 7(9a2 –16b2 )
= 7((3a)2 –(4b)2 )
= 7(3a+4b)(3a-4b)
Using the identity x2 -y2 = (x+y)(x-y)
(iii) 49x2 –36
= (7x)2 -62
= (7x+6)(7x–6)
Using the identity x2 -y2 = (x+y)(x-y)
(iv) 16x5 –144x3
= 16x3 (x2 –9)
= 16x3 (x2 –9)
= 16x3 (x–3)(x+3)
Using the identity x2 -y2 = (x+y)(x-y)
(v) (l+m)2 -(l-m)2
= {(l+m)-(l–m)}{(l +m)+(l–m)}
Using the identity x2 -y2 = (x+y)(x-y)
= (l+m–l+m)(l+m+l–m)
= (2m)(2l)
= 4 ml
(vi) 9x2 y2 –16
= (3xy)2 -42
= (3xy–4)(3xy+4)
Using the identity x2 -y2 = (x+y)(x-y)
(vii) (x2 –2xy+y2 )–z2
= (x–y)2 –z2
Using the identity (x-y)2 = x2 -2xy+y2
= {(x–y)–z}{(x–y)+z}
= (x–y–z)(x–y+z)
Using the identity x2 -y2 = (x+y)(x-y)
(viii) 25a2 –4b2 +28bc–49c2
= 25a2 –(4b2 -28bc+49c2 )
= (5a)2 -{(2b)2 -2(2b)(7c)+(7c)2 }
= (5a)2 -(2b-7c)2
Using the identity x2 -y2 = (x+y)(x-y) , we have
= (5a+2b-7c)(5a-2b+7c)
3. Factorise the expressions.
(i) ax2 +bx
(ii) 7p2 +21q2
(iii) 2x3 +2xy2 +2xz2
(iv) am2 +bm2 +bn2 +an2
(v) (lm+l)+m+1
(vi) y(y+z)+9(y+z)
(vii) 5y2 –20y–8z+2yz
(viii) 10ab+4a+5b+2
(ix)6xy–4y+6–9x
Solution:
(i) ax2 +bx = x(ax+b)
(ii) 7p2 +21q2 = 7(p2 +3q2 )
(iii) 2x3 +2xy2 +2xz2 = 2x(x2 +y2 +z2 )
(iv) am2 +bm2 +bn2 +an2 = m2 (a+b)+n2 (a+b) = (a+b)(m2 +n2 )
(v) (lm+l)+m+1 = lm+m+l+1 = m(l+1)+(l+1) = (m+1)(l+1)
(vi) y(y+z)+9(y+z) = (y+9)(y+z)
(vii) 5y2 –20y–8z+2yz = 5y(y–4)+2z(y–4) = (y–4)(5y+2z)
(viii) 10ab+4a+5b+2 = 5b(2a+1)+2(2a+1) = (2a+1)(5b+2)
(ix) 6xy–4y+6–9x = 6xy–9x–4y+6 = 3x(2y–3)–2(2y–3) = (2y–3)(3x–2)
4.Factorise.
(i) a4 –b4
(ii) p4 –81
(iii) x4 –(y+z)4
(iv) x4 –(x–z)4
(v) a4 –2a2 b2 +b4
Solution:
(i) a4 –b4
= (a2 )2 -(b2 )2
= (a2 -b2 ) (a2 +b2 )
= (a – b)(a + b)(a2 +b2 )
(ii) p4 –81
= (p2 )2 -(9)2
= (p2 -9)(p2 +9)
= (p2 -32 )(p2 +9)
=(p-3)(p+3)(p2 +9)
(iii) x4 –(y+z)4 = (x2 )2 -[(y+z)2 ]2
= {x2 -(y+z)2 }{ x2 +(y+z)2 }
= {(x –(y+z)(x+(y+z)}{x2 +(y+z)2 }
= (x–y–z)(x+y+z) {x2 +(y+z)2 }
(iv) x4 –(x–z)4 = (x2 )2 -{(x-z)2 }2
= {x2 -(x-z)2 }{x2 +(x-z)2 }
= { x-(x-z)}{x+(x-z)} {x2 +(x-z)2 }
= z(2x-z)( x2 +x2 -2xz+z2 )
= z(2x-z)( 2x2 -2xz+z2 )
(v) a4 –2a2 b2 +b4 = (a2 )2 -2a2 b2 +(b2 )2
= (a2 -b2 )2
= ((a–b)(a+b))2
= (a – b)2 (a + b)2
5. Factorise the following expressions.
(i) p2 +6p+8
(ii) q2 –10q+21
(iii) p2 +6p–16
Solution:
(i) p2 +6p+8
We observed that 8 = 4×2 and 4+2 = 6
p2 +6p+8 can be written as p2 +2p+4p+8
Taking Common terms, we get
p2 +6p+8 = p2 +2p+4p+8 = p(p+2)+4(p+2)
Again, p+2 is common in both the terms.
= (p+2)(p+4)
This implies that p2 +6p+8 = (p+2)(p+4)
(ii) q2 –10q+21
We observed that 21 = -7×-3 and -7+(-3) = -10
q2 –10q+21 = q2 –3q-7q+21
= q(q–3)–7(q–3)
= (q–7)(q–3)
This implies that q2 –10q+21 = (q–7)(q–3)
(iii) p2 +6p–16
We observed that -16 = -2×8 and 8+(-2) = 6
p2 +6p–16 = p2 –2p+8p–16
= p(p–2)+8(p–2)
= (p+8)(p–2)
So, p2 +6p–16 = (p+8)(p–2)
1. Carry out the following divisions.
(i) 28x4 ÷ 56x
(ii) –36y3 ÷ 9y2
(iii) 66pq2 r3 ÷ 11qr2
(iv) 34x3 y3 z3 ÷ 51xy2 z3
(v) 12a8 b8 ÷ (– 6a6 b4 )
Solution:
(i)28x4 = 2×2×7×x×x×x×x
56x = 2×2×2×7×x
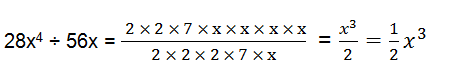
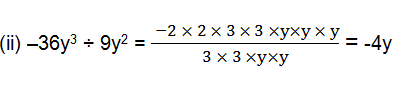
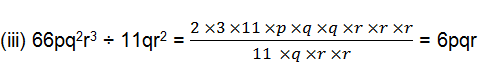
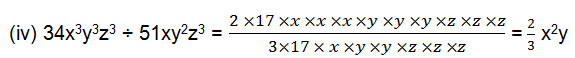
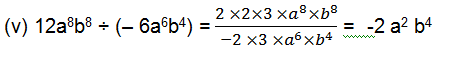
2. Divide the given polynomial by the given monomial.
(i)(5x2 –6x) ÷ 3x
(ii)(3y8 –4y6 +5y4 ) ÷ y4
(iii) 8(x3 y2 z2 +x2 y3 z2 +x2 y2 z3 )÷ 4x2 y2 z2
(iv)(x3 +2x2 +3x) ÷2x
(v) (p3 q6 –p6 q3 ) ÷ p3 q3
Solution:
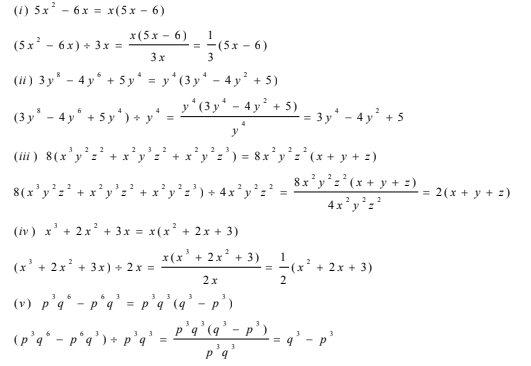
3. Work out the following divisions.
(i) (10x–25) ÷ 5
(ii) (10x–25) ÷ (2x–5)
(iii) 10y(6y+21) ÷ 5(2y+7)
(iv) 9x2 y2 (3z–24) ÷ 27xy(z–8)
(v) 96abc(3a–12)(5b–30) ÷ 144(a–4)(b–6)
Solution:
(i) (10x–25) ÷ 5 = 5(2x-5)/5 = 2x-5
(ii) (10x–25) ÷ (2x–5) = 5(2x-5)/( 2x-5) = 5
(iii) 10y(6y+21) ÷ 5(2y+7) = 10y×3(2y+7)/5(2y+7) = 6y
(iv) 9x2 y2 (3z–24) ÷ 27xy(z–8) = 9x2 y2 ×3(z-8)/27xy(z-8) = xy
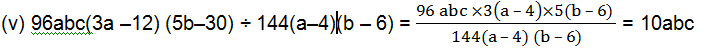
4. Divide as directed.
(i) 5(2x+1)(3x+5)÷ (2x+1)
(ii) 26xy(x+5)(y–4)÷13x(y–4)
(iii) 52pqr(p+q)(q+r)(r+p) ÷ 104pq(q+r)(r+p)
(iv) 20(y+4) (y2 +5y+3) ÷ 5(y+4)
(v) x(x+1) (x+2)(x+3) ÷ x(x+1)
Solution:
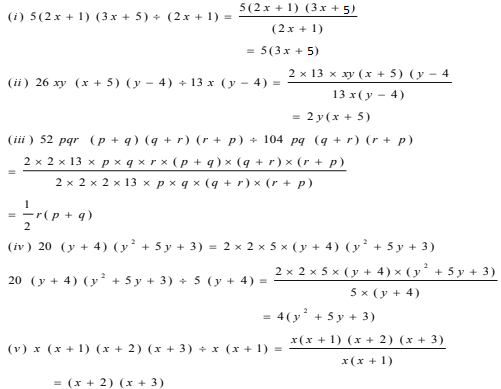
5. Factorise the expressions and divide them as directed.
(i) (y2 +7y+10)÷(y+5)
(ii) (m2 –14m–32)÷(m+2)
(iii) (5p2 –25p+20)÷(p–1)
(iv) 4yz(z2 +6z–16)÷2y(z+8)
(v) 5pq(p2 –q2 )÷2p(p+q)
(vi) 12xy(9x2 –16y2 )÷4xy(3x+4y)
(vii) 39y3 (50y2 –98) ÷ 26y2 (5y+7)
Solution:
(i) (y2 +7y+10)÷(y+5)
First, solve the equation (y2 +7y+10)
(y2 +7y+10) = y2 +2y+5y+10 = y(y+2)+5(y+2) = (y+2)(y+5)
Now, (y2 +7y+10)÷(y+5) = (y+2)(y+5)/(y+5) = y+2
(ii) (m2 –14m–32)÷ (m+2)
Solve for m2 –14m–32, we have
m2 –14m–32 = m2 +2m-16m–32 = m(m+2)–16(m+2) = (m–16)(m+2)
Now, (m2 –14m–32)÷(m+2) = (m–16)(m+2)/(m+2) = m-16
(iii) (5p2 –25p+20)÷(p–1)
Step 1: Take 5 common from the equation, 5p2 –25p+20, we get
5p2 –25p+20 = 5(p2 –5p+4)
Step 2: Factorise p2 –5p+4
p2 –5p+4 = p2 –p-4p+4 = (p–1)(p–4)
Step 3: Solve original equation
(5p2 –25p+20)÷(p–1) = 5(p–1)(p–4)/(p-1) = 5(p–4)
(iv) 4yz(z2 + 6z–16)÷ 2y(z+8)
Factorising z2 +6z–16,
z2 +6z–16 = z2 -2z+8z–16 = (z–2)(z+8)
Now, 4yz(z2 +6z–16) ÷ 2y(z+8) = 4yz(z–2)(z+8)/2y(z+8) = 2z(z-2)
(v) 5pq(p2 –q2 ) ÷ 2p(p+q)
p2 –q2 can be written as (p–q)(p+q) using the identity.
5pq(p2 –q2 ) ÷ 2p(p+q) = 5pq(p–q)(p+q)/2p(p+q) = 5q(p–q)/2
(vi) 12xy(9x2 –16y2 ) ÷ 4xy(3x+4y)
Factorising 9x2 –16y2 , we have
9x2 –16y2 = (3x)2 –(4y)2 = (3x+4y)(3x-4y) using the identity p2 –q2 = (p–q)(p+q)
Now, 12xy(9x2 –16y2 ) ÷ 4xy(3x+4y) = 12xy(3x+4y)(3x-4y) /4xy(3x+4y) = 3(3x-4y)
(vii) 39y3
(50y2
–98) ÷ 26y2
(5y+7)
st solve for 50y2
–98, we have
50y2 –98 = 2(25y2 –49) = 2((5y)2 –72 ) = 2(5y–7)(5y+7)
Now, 39y3 (50y2 –98) ÷ 26y2 (5y+7) =
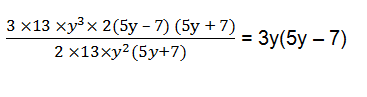
1. 4(x–5) = 4x–5
Solution:
4(x- 5)= 4x – 20 ≠ 4x – 5 = RHS
The correct statement is 4(x-5) = 4x–20
2. x(3x+2) = 3x2 +2
Solution:
LHS = x(3x+2) = 3x2 +2x ≠ 3x2 +2 = RHS
The correct solution is x(3x+2) = 3x2 +2x
3. 2x+3y = 5xy
Solution:
LHS= 2x+3y ≠ R. H. S
The correct statement is 2x+3y = 2x+3 y
4. x+2x+3x = 5x
Solution:
LHS = x+2x+3x = 6x ≠ RHS
The correct statement is x+2x+3x = 6x
5. 5y+2y+y–7y = 0
Solution:
LHS = 5y+2y+y–7y = y ≠ RHS
The correct statement is 5y+2y+y–7y = y
6. 3x+2x = 5x2
Solution:
LHS = 3x+2x = 5x ≠ RHS
The correct statement is 3x+2x = 5x
7. (2x)2 +4(2x)+7 = 2x2 +8x+7
Solution:
LHS = (2x)2 +4(2x)+7 = 4x2 +8x+7 ≠ RHS
The correct statement is (2x)2 +4(2x)+7 = 4x2 +8x+7
8. (2x)2 +5x = 4x+5x = 9x
Solution:
LHS = (2x)2 +5x = 4x2 +5x ≠ 9x = RHS
The correct statement is(2x)2 +5x = 4x2 +5x
9. (3x + 2)2 = 3x2 +6x+4
Solution:
LHS = (3x+2)2 = (3x)2 +22 +2x2x3x = 9x2 +4+12x ≠ RHS
The correct statement is (3x + 2)2 = 9x2 +4+12x
10. Substituting x = – 3 in
(a) x2 + 5x + 4 gives (– 3)2 +5(– 3)+4 = 9+2+4 = 15
(b) x2 – 5x + 4 gives (– 3)2 – 5( – 3)+4 = 9–15+4 = – 2
(c) x2 + 5x gives (– 3)2 +5(–3) = – 9–15 = – 24
Solution:
(a) Substituting x = – 3 in x2 +5x+4, we have
x2 +5x+4 = (– 3)2 +5(– 3)+4 = 9–15+4 = – 2. This is the correct answer.
(b) Substituting x = – 3 in x2 –5x+4
x2 –5x+4 = (–3)2 –5(– 3)+4 = 9+15+4 = 28. This is the correct answer
(c) Substituting x = – 3 in x2 +5x
x2 +5x = (– 3)2 +5(–3) = 9–15 = -6. This is the correct answer
11.(y–3)2 = y2 –9
Solution:
LHS = (y–3)2 , which is similar to (a–b)2 identity, where (a–b)2 = a2 +b2 -2ab
(y – 3)2 = y2 +(3)2 –2y×3 = y2 +9 –6y ≠ y2 – 9 = RHS
The correct statement is (y–3)2 = y2 + 9 – 6y
12. (z+5)2 = z2 +25
Solution:
LHS = (z+5)2 , which is similar to (a +b)2 identity, where (a+b)2 = a2 +b2 +2ab
(z+5)2 = z2 +52 +2×5×z = z2 +25+10z ≠ z2 +25 = RHS
The correct statement is (z+5)2 = z2 +25+10z
13. (2a+3b)(a–b) = 2a2 –3b2
Solution:
LHS = (2a+3b)(a–b) = 2a(a–b)+3b(a–b)
= 2a2 –2ab+3ab–3b2
= 2a2 +ab–3b2
≠ 2a2 –3b2 = RHS
The correct statement is (2a +3b)(a –b) = 2a2 +ab–3b2
14. (a+4)(a+2) = a2 +8
Solution:
LHS = (a+4)(a+2) = a(a+2)+4(a+2)
= a2 +2a+4a+8
= a2 +6a+8
≠ a2 +8 = RHS
The correct statement is (a+4)(a+2) = a2 +6a+8
15. (a–4)(a–2) = a2 –8
Solution:
LHS = (a–4)(a–2) = a(a–2)–4(a–2)
= a2 –2a–4a+8
= a2 –6a+8
≠ a2 -8 = RHS
The correct statement is (a–4)(a–2) = a2 –6a+8
16. 3x2 /3x2 = 0
Solution:
LHS = 3x2 /3x2 = 1 ≠ 0 = RHS
The correct statement is 3x2 /3x2 = 1
17. (3x2 +1)/3x2 = 1 + 1 = 2
Solution:
LHS = (3x2 +1)/3x2 = (3x2 /3x2 )+(1/3x2 ) = 1+(1/3x2 ) ≠ 2 = RHS
The correct statement is (3x2 +1)/3x2 = 1+(1/3x2 )
18. 3x/(3x+2) = ½
Solution:
LHS = 3x/(3x+2) ≠ 1/2 = RHS
The correct statement is 3x/(3x+2)= 3x/(3x+2)
19. 3/(4x+3) = 1/4x
Solution:
LHS = 3/(4x+3) ≠ 1/4x
The correct statement is 3/(4x+3) = 3/(4x+3)
20. (4x+5)/4x = 5
Solution:
LHS = (4x+5)/4x = 4x/4x + 5/4x = 1 + 5/4x ≠ 5 = RHS
The correct statement is (4x+5)/4x = 1 + (5/4x)
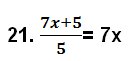
Solution:
LHS = (7x+5)/5 = (7x/5)+ 5/5 = (7x/5)+1 ≠ 7x = RHS